[월간 글립 vol.17 2021년 11월호] 지구는 왜 평평하게 느껴질까? : 곡면과 가우스 곡률
- GLEAP

- 2021년 11월 1일
- 3분 분량
최종 수정일: 2023년 7월 5일
2차원 곡선과 곡률
우리의 주민등록번호, 학번, 혹은 키, 몸무게는 개개인의 고유한 숫자입니다. 이렇게 어떤 사람이나 물체의 특징을 나타내는 데에는 정량화된 숫자가 필요합니다. 평면 위의 도형들도 마찬가지입니다. 도형의 특징으로는 넓이, 둘레 등이 있고, 넓이는 도형이 ‘얼마나 큰지’, 둘레는 도형의 윤곽선이 ‘얼마나 긴지’ 표현해 줍니다. 이제 평면 위의 곡선에 대해서 생각해 봅시다. 평면 위의 곡선은 [그림 1] 과 같이 아주 다양한 형태로 존재할 수 있습니다. 그 중에서도 흔히 접할 수 있는 직선, 원, 타원, 쌍곡선 등이 그 대표적인 예입니다. 그렇다면, 이 곡선이 ‘얼마나 휘었는지’ 를 표현하는 숫자는 무엇일까요? 수학자들은 이러한 숫자, 즉 곡선의 특징을 ’곡률‘이라고 부르기로 하였습니다. 이제 곡선에서 곡률을 정의해 나가는 방법에 대해 알아보도록 하겠습니다.

수학자들은 이러한 숫자, 즉 곡선의 특징을 ’곡률‘이라고 부르기로 하였습니다. 이제 곡선에서 곡률을 정의해 나가는 방법에 대해 알아보도록 하겠습니다. 우선 직선은 전혀 휘어 있지 않기 때문에, 직선의 곡률은 ‘0’입니다. 그렇다면 원의 곡률은 어떨까요? 원의 반지름이 커질수록, 원은 점점 덜 휘어질 것입니다. 직관적으로 생각해 보자면, 우리가 살고 있는 지구는 구형이지만, 지구의 반지름이 너무 큰 나머지 우리는 지구가 평평하다고 느낍니다. 역설적이지만, 우리가 탁구공 위에서 살고 있다면 평평하지 않고 서있을 수도 없겠죠. 즉, 원의 곡률은 반지름이 반비례하게 정의되어야 하고. 수학자들은 이에 착안하여 반지름 r인 원의 곡률을 1/r로 정의하기로 하였습니다. 그렇다면 원, 직선이 아닌 다른 곡선에 대해서는 어떨까요?
다른 특징적인 곡선인 타원에 대해서 생각해 봅시다. 하지만, 타원의 경우 단축에 비해 장축 부근에서 휘어 있는 정도가 더 큼을 알 수 있습니다. 즉, 타원은 원, 직선과 다르게 각 점에서 곡선이 휘어 있는 정도가 다릅니다. 그렇다면 타원의 경우는 원, 직선과 달리 휘어짐 정도를 하나의 숫자로 표현할 수 없는 것일까요?
이러한 문제들은 ‘곡률’을 곡선의 특징이 아닌 ‘곡선의 각 점들’의 특징으로 정의하게 되면 해결할 수 있습니다. 즉 곡선의 각 점들에 대해 그 점 부근에서 곡선이 얼마나 휘어졌는지를, 숫자인 ‘곡률’ 로 정의하는 것이죠. 함수의 개념으로 설명하자면, 각 점이 입력, 곡률이 출력이라고 생각할 수 있습니다.
이제 구체적으로, ‘곡률’이 어떻게 정의되는지 알아봅시다. 곡선의 각 점을 P라고 하면, P를 지나고 곡선에 접하는 원 O를 [그림 2] 와 같이 그릴 수 있습니다. 위에서 언급했듯, 반지름 r인 원의 곡률은 1/r이기 때문에, P에서의 곡률을 (1/O의 반지름)으로 정의할 수 있습니다.

만약 곡선이 점 P에서 덜 휘어있다면, [그림 3] 과 같이 그 점에서 접하는 원 O의 반지름은 클 것입니다. 반대로, 곡선이 점 P에서 많이 휘어있다면 원 O의 반지름은 작을 것입니다. 즉 P에서의 곡률을 (1/O의 반지름)으로 정의하면, 우리가 기존에 생각하였던 ‘얼마나 휘었는지’에 대한 질문이 해결됨을 알 수 있습니다.
3차원 곡면과 가우스 곡률
앞에서는, 2차원 평면에 존재하는 곡선 위의 각 점에 대해서 그 점 근처에서 얼마나 곡선이 휘어있는지를 나타내는 ‘곡률’을 정의하였습니다. 한편, 우리가 사는 세상은 3차원 세상이고, 우리가 살3고 있는 지구의 형태는 구에 가까운 타원체입니다. 아래 [그림 4]처럼 원기둥이나 구 혹은 타원체와 같이 3차원 고안에 있는 2차원의 굽은 모양을 곡면이라 합니다.

위의 문장을 읽은 독자들은 스스로 질문을 던질 수 있을 것입니다. ‘곡면’이 휘어진 정도는 어떻게정의될까요?
기하학 및 여러 분야에 역사를 쓴 가우스(Gauss, 1799~1830)은 이에 대한 답을 해주었습니다. 그는 곡면 위의 각 점에서 휘어진 정도를 나타내는 ‘가우스 곡률’을 정의하였습니다. ‘가우스 곡률’ 은 ‘곡률’ 과 같이, 각 점 근처에서 곡면이 많이 휘었으면 큰 값을 가지고, 반대로 곡면이 덜 휘었으면 작은 값을 가지게 됩니다.
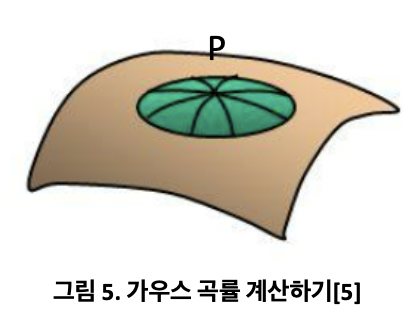
곡률을 정의하는 방식을 대략적으로 살펴보자면, 우선 반지름 r인 구의 가우스 곡률은 1/r^2으로 정의됩니다. 일반적인 경우에서는, 각 점 P에 대해 [그림 5]와 같이 P를 지나고 곡면에 포함되는 곡선들의 곡률을 통해 P에서의 가우스 곡률을 정의할 수 있습니다. 구체적으로는, 그러한 곡률의 최댓값과 최솟값을 곱하여 가우스 곡률을 정의합니다. 이제 글의 주제에 대한 답을 할 수 있습니다. 지구의 반지름은 매우 크므로, 가우스 곡률값은 매우 작게 되고, 그만큼 평평하게 느껴지는 것입니다!
가우스-보넷 정리
위에서 설명하였던 ‘가우스 곡률’ 은 놀라운 성질을 가집니다. 아래 [그림 6]과 같은 2차원 곡면들을 생각해 봅시다.

이들의 공통점은 바로 구멍과 경계선이 없는 곡면이라는 점입니다. 이제 조금 갑작스럽지만, 전체 곡면에 대해 ‘가우스 곡률’ 값을 적분해보겠습니다. 곡면의 각 점 p에 대해 가우스 곡률을 K(p)라고 두고 반지름이 r인 구에 대해 가우스 곡률을 곡면 위에서 적분하면, 다음과 같은 결과를 알 수 있습니다.
그렇다면 다른 곡면들에 대해서는 어떨까요? 놀라운 점은, 항상 [그림 6] 와 같은 곡면들에 대해 가우스 곡률의 적분값은 반지름이 r인 구와 동일하게 항상 4pi 라는 것입니다. 또한 도넛과 같이 구멍이 1개 뚫려 있는 곡면의 경우, 적분 값이 항상 0이 됩니다. 구멍의 개수에 따라서, 가능한 곡면의 모양도 [그림 6] 처럼 천차만별일 것인데 ‘가우스 곡률’ 값을 적분하면 항상 일정한 값이 나오게 되는 것이 신기하죠? 이는 ‘가우스 보넷(Gauss-Bonnet)’ 정리로써, 가우스의 놀라운 발견 중 하나로 현재까지도 기록되고 있습니다.
References
Written by GLEAP 10기 김재연
Edited by GLEAP 학술팀·홍보팀

댓글